Scattering times for electrons in unbiased and biased single and multiple quantum wells

Input files:

• 1DGaAs_AlGaAs_10nmQW_Lifetime.in

• 1DGaAs_AlGaAs_12nmQW_LifetimeFig5_field.in

• 1DGaAs_AlGaAs_SingleQW_7nm.in

• 1DGaAs_AlGaAs_DoubleQW_7nm_nonsymmetric.in

• 1DGaAs_AlGaAs_DoubleQW_LifetimeFig12_field.in

Note

If you want to obtain the input files that are used within this tutorial, please check if you can find them in the installation directory. If you cannot find them, please submit a Support Ticket.

Scope:

This tutorial tries to reproduce the results of [FerreiraBastard1989].

Scattering time as a function of quantum well width

Input file: 1DGaAs_AlGaAs_10nmQW_Lifetime.in

First, we want to study the electron lifetimes (scattering rates) of a single quantum well as a function of quantum well width $QW_width. (Note: Use nextnanomat’s Template feature to automatically sweep over the quantum well width.)

Our quantum well consists of \(GaAs\) that is sandwiched between two \(Al_{0.3}Ga_{0.7}As\) barriers. The material parameters that we are using for this tutorial are identical to the ones used in [FerreiraBastard1989], namely:

• electron mass: \(m_e\) = 0.07 \(m_0\)

• conduction band offset: \(CBO\) = 0.2138 eV

• static dielectric constant: \(\epsilon\) = 12.5

• LO phonon energy: \(\hbar\omega_0\) = 0.036 eV (longitudinal optical phonon)

For the calculations, a grid resolution of 0.1 nm has been used.

quantum{
    region{
        ...
        intraband_matrix_elements{ # calculate dipole moment elements <i|p|j> for intraband transitions
            Gamma{}
        }
        dipole_moment_matrix_elements{ # calculate dipole moment elements <i|x|j> for intraband transitions
            Gamma{}
        }
        transition_energies{ # calculate transition energies
            Gamma{}
        }
        lifetimes{ # calculate lifetimes
            Gamma{}
            phonon_energy = 0.036  # [eV]
        }
    }
}

The following two figures (Figure 2.4.137, Figure 2.4.138) show the conduction band edges and the lowest confined eigenstates (including the square of the wave functions) for a 6 nm and an 18 nm \(AlGaAs\)/\(GaAs\) quantum well.

Figure 2.4.137 Calculated conduction band edge profile (black) and wave functions of confined electron states (\(E_1\) and \(E_2\))

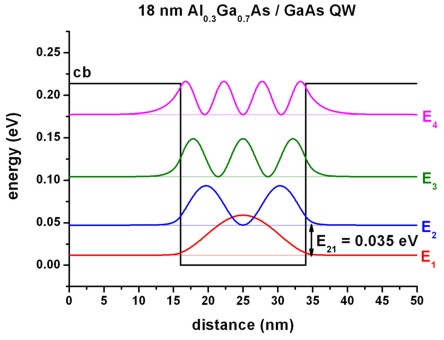
Figure 2.4.138 Calculated conduction band edge profile (black) and wave functions of confined electron states (\(E_1\), \(E_2\), \(E_3\) and \(E_4\)).

The quantum well width can be varied easily by making use of the variable

$QW_width = 10  # (DisplayUnit:nm) (ListOfValues:5.2,5.4,5.6,5.8,6,7,8,10,12,14,15,16,17,18,19,20)

which can be swept automatically using the nextnanomat’s Template feature. Open the input file and select “List of values” and variable “QW_width”.

Figure 2.4.139 shows the electron lifetime of the second eigenstate (\(E_2\) = initial state) to the ground state (\(E_1\) = final state), i.e. the intersubband transition with energy \(E_{21}\) for different quantum well widths. The temperature is set to 0 K.

For quantum well widths smaller than 5.4 nm ([FerreiraBastard1989]: 5.5 nm), only the ground state is confined and \(E_2\) is unbound. For quantum well widths larger than 18 nm ([FerreiraBastard1989]: 17.8 nm), the transition energy \(E_{21}\) is smaller than the LO phonon energy of 36 meV, thus scattering through the emission of an LO phonon is not possible anymore. The nextnano³ calculations are in good agreement with Fig. 3 of [FerreiraBastard1989].

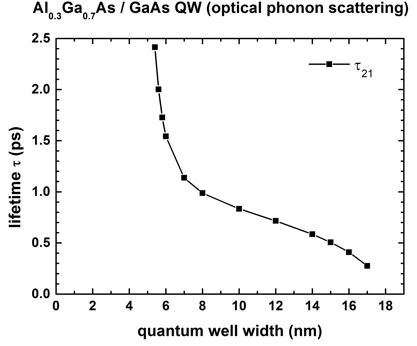
Figure 2.4.139 Calculated lifetimes \(\tau\) as a function of quantum well width

The output of the electron lifetime can be found in this file: bias_00000\Quantum\lifetimes_quantum_region_Gamma.dat.

...
                  Intersubband dipole moment  | < psi_f* | pz | psi_i > |  [h_bar / nm]
------------------|----------------------------------------------------------------------
                                 Oscillator strength []
------------------|--------------|-------------------------------------------------------
                                               Energy of transition [eV]
------------------|--------------|-------------|-----------------------------------------
                                                             m* [m_0]      lifetime [ps]
------------------|--------------|-------------|-------------|-------------|-------------
...
<psi001*|pz|psi002> 0.19717291    0.985747159   0.085864536   0.070000000   0.833765805
...

Here, the shown values for the intersubband transitions correspond to a 10 nm QW.

Scattering times as a function of electric field magnitude

Input file: 1DGaAs_AlGaAs_12nmQW_LifetimeFig5_field.in

This input file will perform a sweep over the electric field strength. Figure 2.4.140 shows the lowest eigenstates of a 12 nm \(AlGaAs\)/ \(GaAs\) QW at an applied electric field of -50 kV/cm. This time the conduction band edge is not flat anymore. It is tilted because of the electric field.

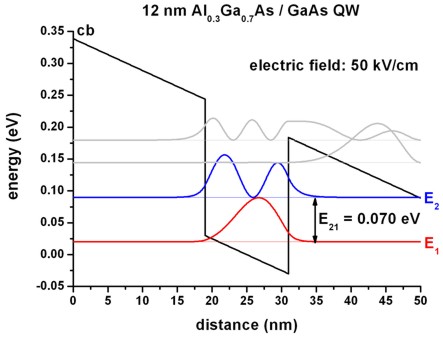
Figure 2.4.140 Calculated conduction band edge profile (black) and wave functions of confined electron states (\(E_1\) and \(E_2\)), when electric field of -50 kV/cm is applied.

The sweep over the electric field magnitude can be done automatically. For these calculations, a grid resolution of 0.10 nm had been used. The nextnano³ calculations presented in Figure 2.4.141 are in reasonable agreement with Fig. 5 in [FerreiraBastard1989].

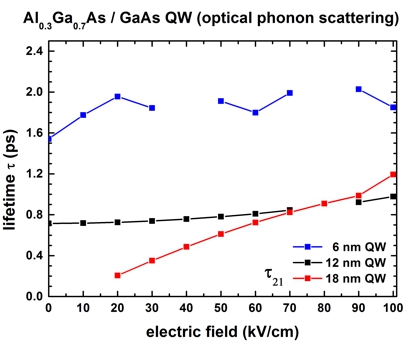
Figure 2.4.141 Calculated lifetimes \(\tau\) in a single quantum well as a function of applied electric field.

Single quantum wells

Input file: 1DGaAs_AlGaAs_SingleQW_7nm.in

The two confined energy levels and wave functions of the 7 nm single quantum well are shown in Figure 2.4.142. The energy of the ground state is 50.4 meV.

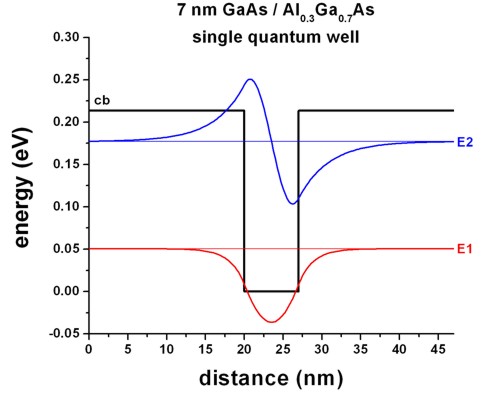
Figure 2.4.142 Calculated conduction band edge profile (black) and wave functions of confined electron states (\(E_1\) and \(E_2\))

Double quantum wells

Input file: 1DGaAs_AlGaAs_DoubleQW_7nm_nonsymmetric.in

Here, we study the electron energy levels of a non-symmetric double quantum well structure as a function of quantum well width of the right quantum well: $right_QW_width. The right quantum well width can be varied easily by making use of the variable:

$right_QW_width = 7     # (DisplayUnit:nm) (ListOfValues:7.0,8.0,10.0,12.5,15.0,17.5,20.0,22.5,25.0,27.5,30.0,35.0,37.5,40.0,45.0,47.5,50.0,55.0,57.5,60.0,65.0,67.5,70.0,75.0,77.5,80.0,85.0,87.5,90.0,95.0,97.5,100.0)

which can be swept automatically using the nextnanomat’s Template feature. Open input file and select “List of values” and variable “right_QW_width”. For the following figures, a grid resolution of 0.25 nm had been used.

Figure 2.4.143 shows the energy levels of a non-symmetric double quantum well structure (\(GaAs\) / \(Al_{0.3}Ga_{0.7}As\)) where the left quantum well always has the width 7 nm, and the right quantum well varies from 7 nm to 100 nm. The two \(GaAs\) wells are separated by a 5 nm \(Al_{0.3}Ga_{0.7}As\) barrier. The figure shows the energy levels as a function of the width of the larger quantum well.

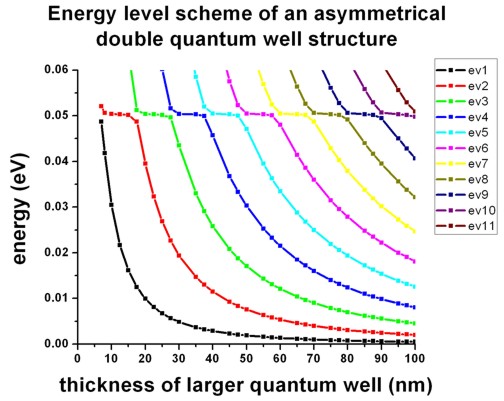
Figure 2.4.143 Calculated energy levels for different energy states as a function of \(L_\mathrm{QW, right}\).

One can see, that for certain widths of the larger quantum well, an anti-crossing due to bonding and anti-bonding states occurs. This happens whenever an eigenstate of the larger well matches the energy of the ground state of the smaller (7 nm) quantum well (which is at 50.4 meV, see example shown above: 1DGaAs_AlGaAs_SingleQW_7nm.in). Our calculations are in very good agreement with Fig. 9 in [FerreiraBastard1989].

The anti-crossing behavior and the plateaus at 50.4 meV of the energy level scheme (see Figure 2.4.143) can be illustrated by plotting the wave functions for different values of \(L_\mathrm{QW, right}\), see Figure 2.4.144, Figure 2.4.145, Figure 2.4.146 and Figure 2.4.147.

Figure 2.4.144 shows a symmetric double quantum well where both wells have the width 7 nm including the wave functions of the lowest confined states. If the barrier between these two wells had been very large, both wells would have had a ground state at 50.4 meV. However, due to the small barrier, coupling between these two wells becomes possible. The two lowest states form a bonding and an anti-bonding state. The bonding state now has a reduced energy of 48.7 meV and the anti-bonding state has an increased energy of 52.1 meV.

Figure 2.4.144 Calculated conduction band edge profile (black) for symmetric double quantum well: \(L_\mathrm{left}\) = 7 nm and \(L_\mathrm{right}\) = 7 nm, with wave functions of confined electron states.

Figure 2.4.145 shows a non-symmetric double QW where the right QW has a width of 12.5 nm. In this case, the ground state can be found in the larger well, the second state in the 7 nm QW, whereas the third eigenstate is again localized in the larger well. Here, no bonding or anti-bonding states exist.

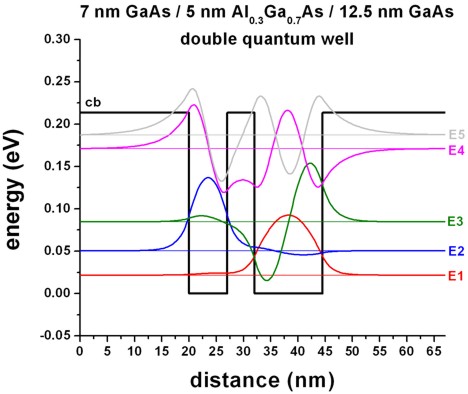
Figure 2.4.145 Calculated conduction band edge profile (black) for non-symmetric double quantum well: \(L_\mathrm{left}\) = 7 nm and \(L_\mathrm{right}\) = 12.5 nm, with wave functions of confined electron states.

Figure 2.4.146 shows a non-symmetric double QW where the right QW has a width of 17.5 nm. In this case, the ground state can be again found in the larger well (similar to Figure 2.4.145), but this time, the third state of moves down in energy and couples to the 7 nm ground state of the left well (compare with Figure 2.4.145). This coupling leads to the formation of a bonding and an anti-bonding states.

Figure 2.4.146 Calculated conduction band edge profile (black) for non-symmetric double quantum well: \(L_\mathrm{left}\) = 7 nm and \(L_\mathrm{right}\) = 17.5 nm, with wave functions of confined electron states.

Figure 2.4.147 shows a non-symmetric double QW where the right QW has a width of 25 nm. In this case, the ground state and the second state can be found in the larger well, whereas the third eigenstate is localized in the smaller (7 nm) well. The forth eigenstate is localized in the larger well. Again, no bonding or anti-bonding states exist

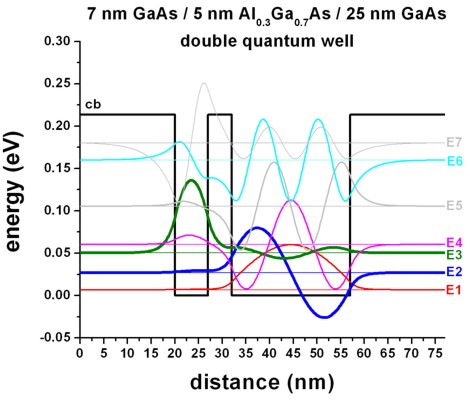
Figure 2.4.147 Calculated conduction band edge profile (black) for symmetric double quantum well: \(L_\mathrm{left}\) = 7 nm and \(L_\mathrm{right}\) = 25 nm, with wave functions of confined electron states.

Biased double quantum well

Input file: 1DGaAs_AlGaAs_DoubleQW_LifetimeFig12_field.in

Figure 2.4.148 shows the lifetime of the 2 \(\rightarrow{}\) 1 transition (“ground state of left quantum well to ground state of right quantum well transition”) as a function of electric field. The variable \(d\) is the thickness of the left well and the barrier region. The right well is assumed to have the same thickness as the left quantum well, i.e. \(d\)/2.

The parameter \(d\) can be varied easily by making use of the variable

$QWBarrierThickness = 6     # (DisplayUnit:nm) (ListOfValues:6,9)

which can be swept automatically using the nextnanomat’s Template feature. Open input file and select “List of values” and variable “QWBarrierThickness”.

There seems to be qualitative agreement to Fig. 12 in [FerreiraBastard1989]. For \(d\) = 9 nm, the LO phonon emission is forbidden for electric fields smaller than ~ | 40 kV/cm | because the transition energy is smaller than the LO phonon energy of 36 meV.

Figure 2.4.148 Calculated lifetimes \(\tau\) in a single quantum well as a function of applied electric field.

Last update: nn/nn/nnnn