nextnano³ - Tutorial

3D Tutorial

Quantum dot molecule

Author: Stefan Birner

==> This is the old website: A new version of this tutorial can be found here.

==> 3DQD_molecule_cuboid_asymmetric_nn3.in / *_nnp.in - input file for the nextnano³ and nextnano++ software

Quantum dot molecule

• In this tutorial, we study two coupled quantum dots (QDs), i.e. two "artificial atoms" that form an "artificial molecule".
  The two QDs are asymmetric and differ with respect to their height (4 nm and 6 nm).
• We keep things simple by using cuboidal shaped GaAs QDs surrounded by Al_0.35Ga_0.65As barriers, i.e. we neglect strain and piezoelectric effects which is reasonable as the two materials GaAs and Al_0.35Ga_0.65As have pretty similar lattice constants.
  We also neglect the wetting layers and excitonic effects.
• In order to keep the CPU time to a minimum, we do not use the k.p approximation, i.e. we use for both electrons and the heavy hole a single-band effective mass approximation for the Schrödinger equation (parabolic and isotropic effective mass tensor).
  Nevertheless, this is sufficient to show some basic quantum physical effects of this QD molecule.
  We use different electron and hole masses in the barrier and well material, respectively.
• The left   QD has the dimensions 10 nm x 10 nm x 4 nm (smaller dot).
  The right QD has the dimensions 10 nm x 10 nm x 6 nm (larger   dot).
  The two QDs are separated by a 2 nm Al_0.35Ga_0.65As barrier.
• The grid resolution is 0.5 nm (rectangular tensor grid). This leads to a 3D Schrödinger matrix of dimension 50,225.
• We apply Dirichlet boundary conditions to the Schrödinger equation, i.e. the wave functions are allowed to penetrate the following distances into the barrier material (on each side):
  - along the x and y directions: 4 nm
  - along the z direction: 4.5 nm
• We vary the electric field along the growth direction (z axis) in steps of -2.5 kV/cm, i.e. from 0 kV/cm to -40 kV/cm.
• The following figures show the square of the electron (left side) and heavy hole (right side) wave functions (isovolumes of 25 % of psi²) for different applied electric fields (0 kV/cm, -17.5 kV/cm, -40 kV/cm).
  A slice through the conduction and valence band edges along the growth direction through the center of the QDs is also shown.

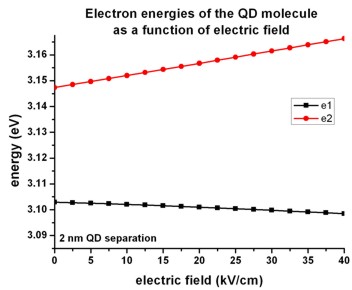
• The following figure shows the electron energies of the ground state (e1) and the first excited electron state (e2) of the QD molecule.
  The ground state (e1) is always located in the larger QD (right side) whereas the first excited electron state (e2) is always located in the smaller QD (left side).
  The third and the forth eigenstate (e3, e4) are degenerate (not shown) because our QD molecule has a symmetry with respect to the x and y coordinates. They are always located in the right QD.
  
  
   
• The following figure shows the heavy hole energies of the ground state (h1) and the excited hole states (h2, h3, h4, h5) of the QD molecule.
  In contrast to the electrons, the hole coupling between the two QDs is much stronger due to the smaller barrier height.
  At -17.5 kV/cm anticrossing between the states occur due to the formation of bonding and antibonding states (see figures of the hole wave functions further below).
  
  
   
• The following figure shows the square of the lowest five hole wave functions (isovolumes of 2 % of psi²) at an electric field of -17.5 kV/cm.
   

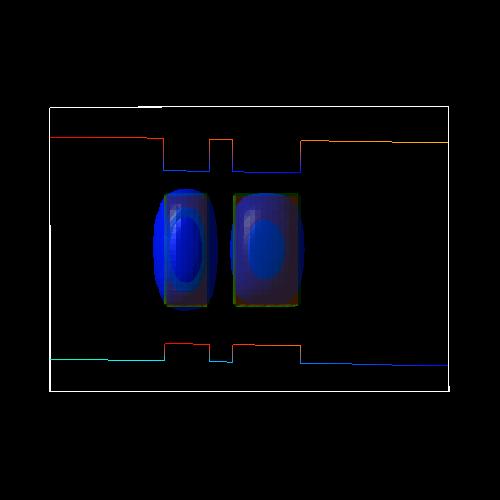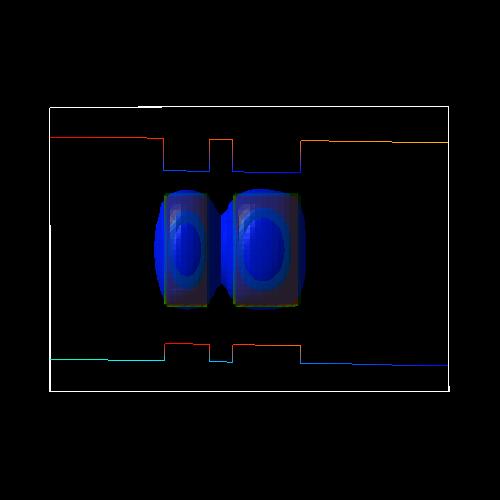
  heavy hole (h1) ground state at -17.5 kV/cm (bonding)	heavy hole (h2) first excited state at -17.5 kV/cm (antibonding)
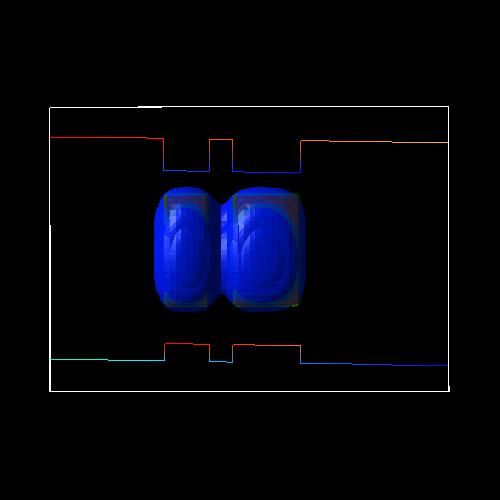
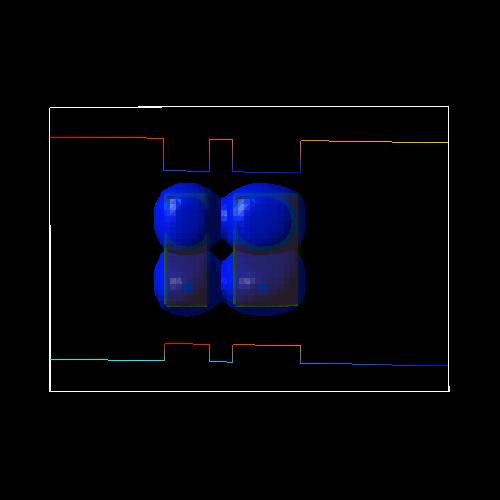  heavy hole (h3) state at -17.5 kV/cm (bonding)	heavy hole (h4) state at -17.5 kV/cm (bonding)
  Note that heavy hole (h3) and heavy hole (h4) are degenerate due to the symmetry with respect to the x and y axis.
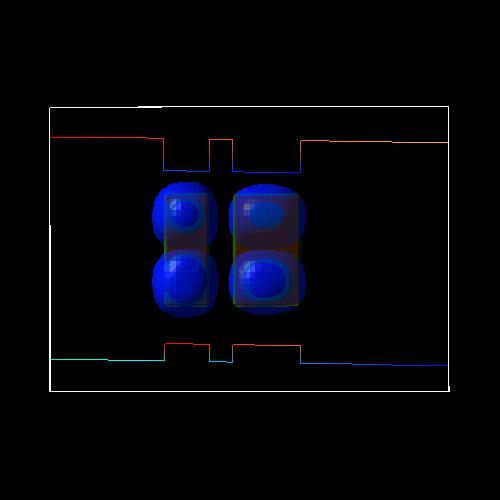  heavy hole (h5) state at -17.5 kV/cm (antibonding)	heavy hole (h6) state at -17.5 kV/cm is also antibonding and degenerate with (h6) due to (x,y) symmetry (not shown)

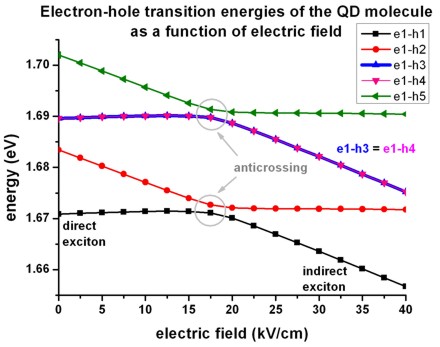
• The following figure shows the five lowest electron-hole transition energies of the QD molecule as a function of electric field.
  For fields smaller than -17.5 kV/cm a direct (bright) exciton is the ground state (both electron and hole wave function are located in the larger QD (right side), whereas for fields larger than -17.5 kV/cm an indirect (dark) exciton is the ground state where the electron is located in the larger QD (right side) and the hole is located in the smaller QD (left side).
  Therefore, the nature of the QD molecule ground state changes from direct to indirect.
  
  At -17.5 kV/cm anticrossings occur due to the bonding and antibonding character of the hole wave functions.
  
  
   
• To understand the strength of the optical transitions we have to evaluate the matrix elements of the envelope functions, i.e. the spatial overlap integral over the electron and hole wave functions.
  
       integral  (psi_el,i*(x)  psi_hl,i(x) dx)
  
  As expected, the direct exciton is much brighter than the indirect (dark) exciton.
  
  
   
• Some of the material parameters that are used in this tutorial are based on the paper of
  
      M. Grundmann, D. Bimberg
      Formation of quantum dots in twofold cleaved edge overgrowth
      Phys. Rev. B 55 (7), 4054 (1997).
  
  i.e. they are the same as in the 3D CEO QD tutorial (apart from the effective masses).